FoxAndCity
作者:熊云帆
关键词:网络流
题目简述
给定一张无向图,每条边的边权都是,所有的点用~编号。每个点的点权定义为这个点到号点的最短路长度。每个点还有一个值。
你可以通过给这张图添上若干条边来改变一些点的点权。要求最小化。
算法一
对于一个合法的最终状态,一定满足:
- 若在原图中i到j有连边,有
对于一个满足上述条件的数组,按照下述方法一定可以构造出一个合法的图:
- 按照的值排序建出分层图。
- 每个点向它的前一层,当前层和后一层连边。
因此,原问题等价于构造一个满足上述条件的数组使得的值最小。
直接枚举所有合法情况。按照拓扑序枚举时,每个至多只有三种取值,状态数是,需要判断是否合法,计算答案。
时间复杂度:。
算法二
考虑用网络流来解决这个问题。
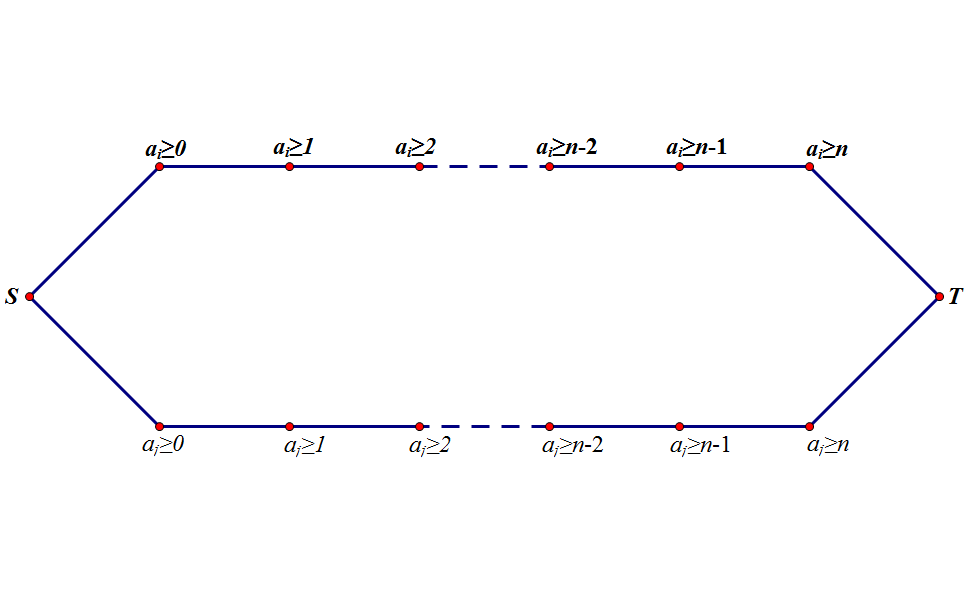
如图,和表示源点和汇点。若和联通则表示第个点的值至少位。
注:图中的边为从左到右的有向边。
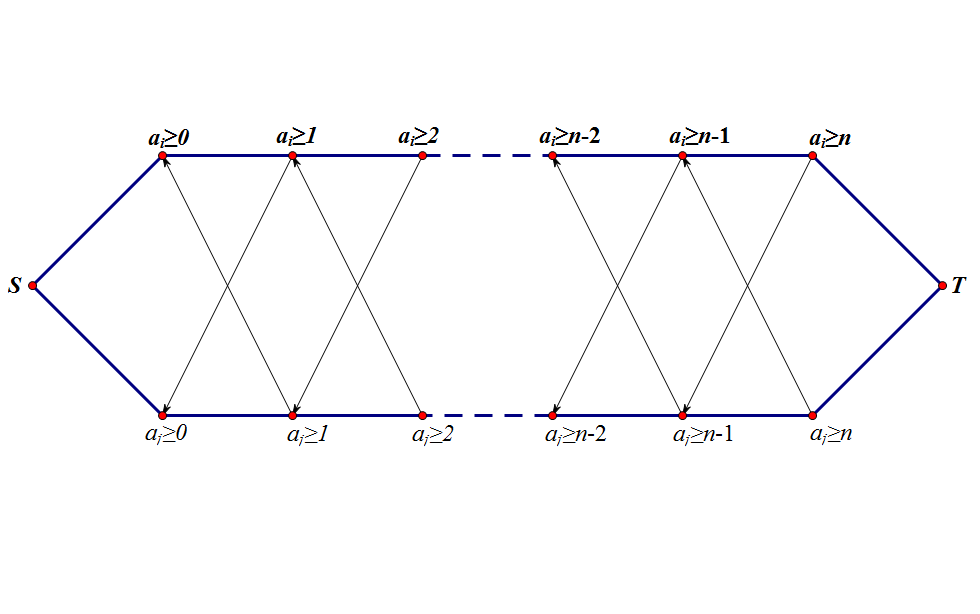
如图,若点和点有边相连,则连出所有的边和。
这样,我们就可以保证若边被割,则 中有且只有一条边被割开。
特别地,当时,为;当时,为。
例如:
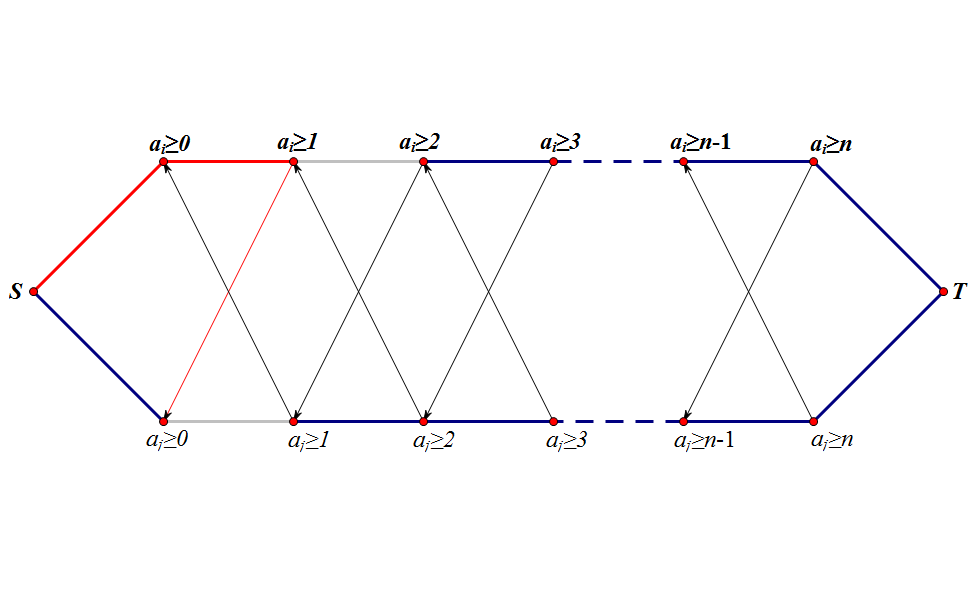

从图中我们可以看到,如果对应的中的三条边中有一条边未在割中出现,那么中被割掉的那条边是无效的。所以对于最小割中的任意一条边,其对应的三条边中一定有一条在割中出现。
并且,这不但是必要条件,也是充分条件。考虑反证法:如果存在从到的通路,那么考虑最后一条边所属于的点。设上一个点为,因为无法走到,所以矛盾。
图建出来后跑最小割即可。
点数,边数,所以复杂度。
时间复杂度:。