CurvyonRails

作者：吕欣

关键词：图论建模，二分图，费用流

题意简述

给定一个 $n\times m$ 的棋盘，标记棋盘上的一些格为城镇，再标记城镇中的一些为关键格。你需要铺设轨道，有以下要求：

1. 非城镇上不允许铺设轨道。
2. 每个城镇铺一段轨道，连接它的四个边界中的两个。
3. 每段轨道需要连接另外两段轨道。

注意：所有城镇不必互相连通。不难想象，棋盘上的城镇被连接成了若干个互不相交的环。

你需要尽可能地在关键格上铺设弯轨道。因此，对于一种合法的方案，定义它的费用为“铺设了直轨道的关键格的个数”。

判断解的存在性，在此基础上，最小化铺设轨道的费用。

约定：$n,m\leq 25$

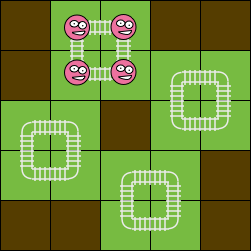
下图展示了同一个棋盘上的两种不同的方案，费用分别为 $1$ 和 $0$。

初步建模

这道题需要稍稍脑洞大开的建图。

首先，不考虑费用的问题，如何判断解的存在性？

由于棋盘天然是二分图，对棋盘进行黑白染色之后，我们铺设的轨道总是连接着一个黑点和一个白点，由于不考虑城镇的连通性，这实际上是一个匹配问题，考虑建图：

1. 对于每个城镇，$S$ 向黑格连流量为 $2$ 的边，白格向 $T$ 连流量为 $2$ 的边，代表每个城镇需要和相邻的两个城镇匹配；
2. 对于相邻的两个城镇 $i$, $j$，不妨设 $i$ 为黑格，$i$ 向 $j$ 连接流量为 $1$ 的边，代表它们可以匹配。

对这张图求 $S$ 到 $T$ 的最大流，检查 $S$ 连出的边和连入 $T$ 的边是否满流，即可判断解的存在性。

另外，注意到黑白点数不一致时，一定无解，而黑点数=白点数时，$S$、$T$的连出、连入的边全部满流等价于 $流量=黑点数*2$，由此可以简化代码实现。

最小化费用

如何最小化费用呢？

考虑如何区分弯轨道和直轨道，不难发现，弯轨道总是匹配了一个同行的点，和一个同列的点。与此相反，直轨道总是匹配了两个同行/同列的点，我们考虑如下的费用流建图。

1. 首先 $S$ 向黑格连边、白格向 $T$ 连边与上述方法类似。

2. 考虑拆点，对每个城镇 $i$，拆出两点 $i_r$，$i_c$，代表行上的匹配和列上的匹配，不妨设 $i$ 为黑格，白格的情况把边反向即可。

   • 对关键格，$i$ 向 $i_r$、$i_c$ 分别连两条边，两条边的$(流量, 费用)$ 分别为 $(1,0)$ 和 $(1, 1)$，代表如果 $i$ 匹配了两个同行/同列的点，则需要支付一点费用。
   • 对非关键格，$i$ 向 $i_r$, $i_c$ 分别连一条流量$2$，费用$0$的边，代表 $i$ 可以自由匹配两个点。

3. 对同一行上相邻的点 $i_r$ 和 $j_r$，不妨设 $i_r$ 为黑格，$i_r$ 向 $j_r$ 连一条流量$1$，费用$0$的边，列上类似。

对这个图求最小费用最大流，检查流量的大小，即可判断解的存在性。在此基础上，求得的费用值就是最小费用。

上述方法中的一些点和边不是必要的，但这样的建图实现方便、容易理解，且足以胜任题目的数据规模。

效率：

算法的复杂度瓶颈在于费用流的计算。
图的点数是 $O(nm)$ 级别的，边数和点数同级，因此：

时间复杂度 $O(\mathbf{costflow}(nm, nm))$
空间复杂度 $O(nm)$